قبل الاطلاع على محتوى هذه المقالة يمكن العودة للمقالات السابقة في هذه السلسلة:
1-نظرية التوازن: مقدمة
2-نظرية التوازن: البدايات الأولى
3-مفهوم نظرية التوازن
4-نظرية الرسم البياني والتوازن
تُشير نظرية التوازن الاجتماعي (social balance theory) إلى توازن أو عدم توازن العلاقة العاطفية في العلاقة الثنائية أو الثُلاثية، حيث تُزودنا هذه النظرية بأداة لتحليل النظام الاجتماعي، وكيف أن العلاقة العاطفية عبر الأفراد تتَّجه نحو حالة التوازن الذي يمكن أن يُقوِّي التفاعل الاجتماعي (مستويات الثنائيات) أو التضامن (solidarity) (في المستوى الكبير) أو بدء الانقسام أو الانفصال للمجموعات الفرعية في شبكات الشخصية الاجتماعية، فقد ينتج عن العواطف انقسام اجتماعي (social mitosis) ويمكن تعريفه بأنه ظهور مجموعتين، فالكُره يوجد بين مجموعتين فِرعِيَّتين في إطار المجموعات المتحابَّة.

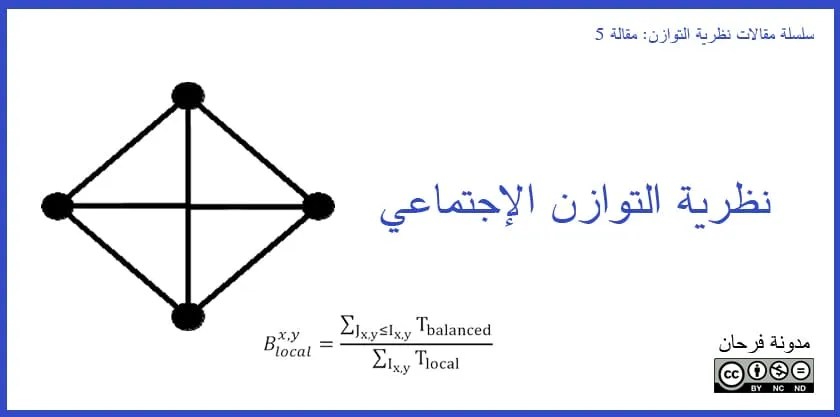
فالعلاقات العاطفية للأفراد (مُحدَّدة كثُلاثية وثُنائية) تُظهِر التوازن الجماعي/التراكمي للمجموعة، بعبارة أُخرى، تكمن المهمة هنا في الانطلاق من التوازن على المستوى الجزئي (على المستوى الثُنائي/الثُلاثي) باتجاه التوازن على المستوى الجماعي/التراكمي، فالأفراد يميلون لاختيار حالة التوازن في علاقاتهم الشخصية، وهذا ينشأ عن الضغط أو التوتُّر الناتج من حالة عدم التوازن في علاقاتهم الشخصية، والتي تدفع الفرد إلى تغيير علاقة عاطفته نحو تشكيل التوازن أو نحو توتُّر أقل، فالعلاقات العاطفية عبر الأفراد يمكن افتراضها كشبكة شخصية اجتماعية، وهنا فإن نظرية التوازن الهيكلي (structural balance theory) تُظهر كيف أن التغيُّر في إشارة إحدى الثنائيات تؤدي إلى تغيُّر التوازن بالنسبة للرسم البياني كاملاً، وهنا نحن نقدم شبكة شخصية اجتماعية (social interpersonal network) عبر الأفراد في مجموعة كبيرة كشبكة مكونة من ثلاثيات مُمكنة، ومن ناحية أُخرى كل ثُلاثية محلِّية (local) تتكون من ثلاثة ثنائيات، وبمعرفة النمط الأولي لكل العلاقات الثُنائية يمكننا أن نُقرِّر ما إذا كانت الثُلاثيات المُتشكِّلة متوازنة أو لا، وهنا نستعمل مؤشِّر التوازن التراكمي (global balance index) الذي يُعرَّف بأنَّه نسبة عدد الثُلاثيات المتوازنة مقسوم على كل الثُلاثيات المُشكَّلة المحتملة، ومؤشِّر التوازن المَحلِّي (local balance index)، الذي يُعرِّف بأنه النسبة بين عدد الثلاثيات المتوازنة المُشكَّلة من ثُنائية والعدد الحالي لجميع الثُلاثيات المُشكَّلة من نفس الثُنائية. المؤشِّر السابق يُستخدم لقياس توازن أو عدم توازن الشبكة (محلِّياً أو تراكميَّاً)، فالشبكة المتوازنة تراكميَّاً سيكون لها مؤشِّر توازن يساوي 1.
باقي محتوى هذه المقالة حصري بالمشتركين بالمدونة، يمكن الاشتراك مجاناً بالقائمة البريدية للمدونة للوصول لجميع مقالات نظرية التوازن، كما يمكن طلب النسخة الإلكترونية الكاملة لكتاب “مقدمة في نظرية التوازن” عبر الرابط التالي:


الاشتراك لمواصلة القراءة
اشترك للوصول إلى الجزء المتبقي من هذه التدوينة ومحتوى آخر للمشتركين فقط.